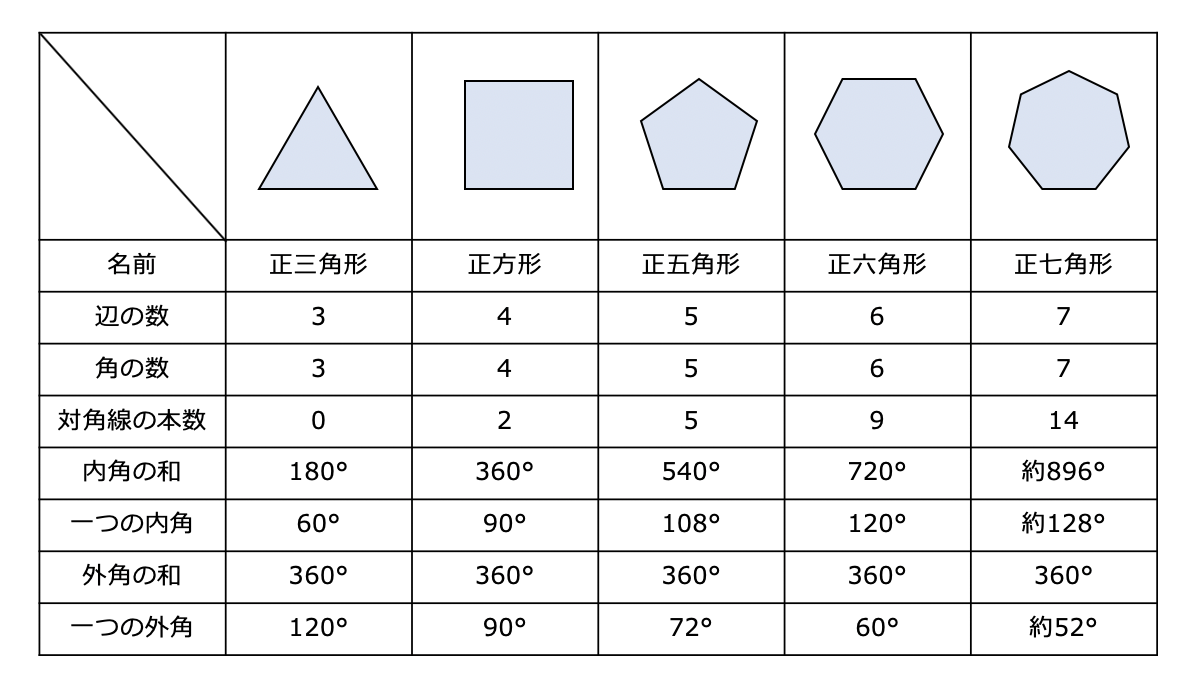
正n角形の辺の長さから面積,周囲の長さ,頂点の角度, 0925 男 / 30歳代 / 会社員・公務員 / 役に立った /正n角形の外角の和は360度 正10角形の外角は360÷10=36度 正10角形の内角は=144度←答え 180×(n 2)÷n だったような気がします。 今回の場合正十角形なのでnに10を入れたら求めれます 正十二内角 の 和 は1980°、 対角線 の本数は65本である。 正十三角形においては、 中心角 と 外角 は27 ° で、内角は152 °となる(下線部は循環節)。 一辺の長さが a の正十三角形の 面積 S は S = 13 4 a 2 cot π 13 ≃ a 2 {\displaystyle S= {\frac {13} {4}}a^ {2}\cot {\frac {\pi } {13}}\simeq \,a^ {2}} となる。

三角形的內角與外角n 邊形的內角和三角形的外角和定理n 邊形的外角和三角形的內角和定理正n邊形的內角與外角三角形的外角定理
正10角形 外角
正10角形 外角-内角の和 三角形の内角の和は \(180°\) 四角形の内角の和は \(360°\) これは小学校で学習しましたし、暗記もできていることと思います。 では、 五角形の内角の和は何度でしょうか。 六角形の内角の和は何度でしょうか。 七角形の内角の和は何度でしょうか。正n角形の内角の大きさは{180(n2)}/n 度、外角の大きさは360/n 度です。具体例を通じてその理由を見ていきましょう。 算数から高度な数学まで、網羅的に解説したサイト 正多角形の内角と外角の大きさ 具体例で学ぶ数学 > 図形 > 正十角形の外角の大きさは 360



十九角形 Wikipedia
これは多角形の外角の和の研究です。 多角形の内角の和は変化しますが、外角の和は一定です。 つまり、内角の和の公式よりも、外角の和の方が本質的だということです。 それを直観的に証明してみましょう。 そして、このことから、外角から正多角形を作ることができます。まずは正十角形の外角1つ分の大きさを求めます。 $$360 \div 10=36°$$ 内角は\(180(外角)\)より $$=144°$$ となります。 内角の和を考えて求める場合には $$180 \times (102)=1440°$$ 内角の和をこのように求めて 10で割ってやれば求めることができます。 $$1440 \div 10 =144°$$正10角形は2等辺三角形が10個 出来ますよね? 中心に集まっている頂点の角は360°をその個数で割ったものに等しくなります。 5角形なら72°、10角形なら36°。 3角形の内角の和は180°なので、2等辺三角形の残りの角の和は 180°72°=108°五角形 180°36°=144°10角形
正5 角形が並んでできる穴の縁である図形(正10 角形)の1つの外角は、上の図から 5 に なっている。どの外角も、これと同じ状況であるから、この穴の縁を歩いている人が、m 個の角 で進行方向を変化させる角度の合計は、 5 £ m となる。180(102)=180×8=1440° 正八角形の1つの外角 多角形の外角の和はどれも360°なので 360°÷8=45° 確認 答表示 ① 十二角形の内角の和を求めよ。 ② 正九角形の一つの外角は何度か。 答①1800° ②40° 内角の和、外角の和 例題と練習問題 例題6 ∠x= 7 ∠x= 8 右の正六角形で ∠x= ∠y= 9 右の正十角形で ∠x= ∠y= 10 1つの外角が18°になる正多角形は,正x角形である。 x= トップに戻る 前ページに戻る 次ペ-ジに進む 答のペ-ジに進む
なぜ三角形の内角の和が180度になるのか? Web検索してもなかなかよい証明(説明)が見つからないので書いてみました。 錯角や同位角を使った証明も、錯角や同位角への疑問を生みスッキリしませんよね。 ヒントは外角の和にあります。正多角形の外角の大きさをどうしても知りたい! こんにちは!この記事をかいているKenだよ。鍋つくりたいね。 正多角形の外角の大きさ がわからない・・・・・ そんなときは公式をつかえば一発。 正n角形の外角の1つの大きさは、 360°/n になるんだ。正十五角形の1つの外角の大きさの求め方を教えて下さい! 0 この回答がベストアンサーに選ばれました。 otas 5年弱前 正多角形の外角の和って360度ですね。 という事は、正三角形の一つの外角は360÷3



十九角形 Wikipedia



十六边形 维基百科 自由的百科全书
③正12角形の1つの内角の大きさは? 解法1:外角を用いた解法 正12角形の外角の大きさは全て等しく、外角の和は360°。 だから、1つの外角の大きさは360°÷12=30° 1つの頂点において、内角外角=180°となるので正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるねタヌキ 正5角形の内角の和を計算すると 5角形は三角形3つに分けることができるから 180×3=540°となります。 キツネ 正5角形は5つの等しい内角でできていて この5つの角度の和は、540°だから、 1つの角は



外角公式 内角和公式和外角和公式 正多边形外角和公式 正n边形的内角和公式



100以上正12角形三角形 壁紙引用画像hd
多角形の外角の和が360°になることの説明。 まず四角形で考えてみましょう。 図に示した赤い角度が外角です。さらに内角を青で表示します >>内角 内角と、それに隣り合う外角の和は180°です。図では隣り合っている赤と青のそれぞれが1組180°です。正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるね(3) 正五角形では5つの外角の和は ゜だから1つの外角は ゜ したがって1つの内角は ゜です. 何角形でも外角の和は360° 正五角形だから1つの外角は360°÷5=72° したがって,1つの内角は180°−72°=108° この問題は五角形の内角の和が540°になることを使っても求められるが,初めの2つの空欄を



十边形怎么画简单 第1页 一起扣扣网



壁紙押入れ 最高50 正12 角形
正5 角形が並んでできる穴の縁である図形(正10 角形)の1つの外角は、上の図から 5 に なっている。どの外角も、これと同じ状況であるから、この穴の縁を歩いている人が、m 個の角 で進行方向を変化させる角度の合計は、 5 £ m となる。タヌキ 正5角形の内角の和を計算すると 5角形は三角形3つに分けることができるから 180×3=540°となります。 キツネ 正5角形は5つの等しい内角でできていて この5つの角度の和は、540°だから、 1つの角は(3) 十六角形の外角の和は何度か。 (4) 十八角形の外角の和は何度か (5) 内角の和が2340°である多角形は何角形か。 (6) 内角の和が1800°である多角形は何角形か。 2410 多角形の内角と外角の和 a 30° b c 2 それぞれの正多角形について、下の表の空らんをうめ


第四章多边形内角和



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码
正十五角形の1つの外角の大きさの求め方を教えて下さい! 0 この回答がベストアンサーに選ばれました。 otas 5年弱前 正多角形の外角の和って360度ですね。 という事は、正三角形の一つの外角は360÷3正n角形の内角の大きさは{180(n2)}/n 度、外角の大きさは360/n 度です。具体例を通じてその理由を見ていきましょう。 算数から高度な数学まで、網羅的に解説したサイト 正多角形の内角と外角の大きさ 具体例で学ぶ数学 > 図形 > 正十角形の外角の大きさは 360中学生の時の話です。 小学生までは三角定規とコンパスで正三角形や正方形、六角形を書く方法などを学びます。 中学生になると、こんどは分度器を使って正n角形を書くことを学びました。このとき書けるのは、正三角形、正四角形


Scratch3数学之美01 绘制正多边形 简书



三角形外角和2种方法 三人行教育网 Www 3rxing Org
これは多角形の外角の和の研究です。 多角形の内角の和は変化しますが、外角の和は一定です。 つまり、内角の和の公式よりも、外角の和の方が本質的だということです。 それを直観的に証明してみましょう。 そして、このことから、外角から正多角形を作ることができます。正5 角形が並んでできる穴の縁である図形(正10 角形)の1つの外角は、上の図から 5 に なっている。どの外角も、これと同じ状況であるから、この穴の縁を歩いている人が、m 個の角 で進行方向を変化させる角度の合計は、 5 £ m となる。多角形の外角の和が360°になることの説明。 まず四角形で考えてみましょう。 図に示した赤い角度が外角です。さらに内角を青で表示します >>内角 内角と、それに隣り合う外角の和は180°です。図では隣り合っている赤と青のそれぞれが1組180°です。


正十五角形の1つの内角の大きさを求めなさい 内角の和が3240 である Yahoo 知恵袋



例題 正12 邊形的內角外角 Youtube
正n角形の外角の和は360度 正10角形の外角は360÷10=36度 正10角形の内角は=144度←答え 180×(n 2)÷n だったような気がします。 今回の場合正十角形なのでnに10を入れたら求めれます 正十二180(102)=180×8=1440° 正八角形の1つの外角 多角形の外角の和はどれも360°なので 360°÷8=45° 確認 答表示 ① 十二角形の内角の和を求めよ。 ② 正九角形の一つの外角は何度か。 答①1800° ②40° 内角の和、外角の和 例題と練習問題 例題円を使って正六角形をかく。 また,その方法で正六角形がかける理由を考える。 スクラッチで正多角形をかく。(本時) ・正三角形,正五角形,正六角形 ・内角と外角 ・正多角形の性質と定義 ・正n 角形を推論


初中数学应用题傲德 腾讯视频



壁紙押入れ 最高50 正12 角形


実践例 プログラミングで正多角形を学ぶ 山﨑智仁 Tomohito Yamazaki Note


正十角形の1つの外角の大きさはどう求めるか教えてください 多 Yahoo 知恵袋



青少年编程 用python探究数学 3 老齐教室


Scratch考级40图 图10 绘制正五边形 青少年编程学习专栏 Csdn博客


第四章多边形内角和


多边形的外角和 腾讯视频



十边形英文


正多邊形 定義 相關概念 外接圓 內切圓 內角 外角 中心角 面積 對稱軸 鑲嵌規 中文百科全書



三角形的內角與外角n 邊形的內角和三角形的外角和定理n 邊形的外角和三角形的內角和定理正n邊形的內角與外角三角形的外角定理



探究神奇的几何世界 相关定理合集第一部分 网易订阅



正十二角形の一つの内角はどうやって求めればいいのか教えてください Clear



正多边形面积计算公式


10边形内角和是多少 初三网



壁紙押入れ 最高50 正12 角形


多边形的内角和 Ppt课件下载 第一ppt



正方形的外角和是多少度



正五角星每个锐角度数正五角星的每一个锐角的度数



08年学业考试复习第一轮第四章基本图形一知识回顾多边形上或内部一点与多边形各顶点的连线将多边形分割成若干个小三角形如图给出了四边形的三种不同的分割方法分别将四边形分割成了2个3个4个小三角形


正多边形外角公式 多边形外角和公式 尚书坊



三角形的內角與外角n 邊形的內角和三角形的外角和定理n 邊形的外角和三角形的內角和定理正n邊形的內角與外角三角形的外角定理



Scratch繪製圖形 正多邊形 計算正多邊形的外角 範本試玩 Altohorn Teach Infoedu



多边形的内角



八年级下册第五章平行四边形5 1多边形同步练习1下载 在线阅读 爱问共享资料



96多边形的内角和与外角和 97平面图形的密铺 Ppt课件 文库吧



內角和外角 幾何學小作品 Internal And External Angles 资


Scratch3数学之美01 绘制正多边形 简书



正十边形的画法步骤图 第1页 一起扣扣网



青少年编程 用python探究数学 3 老齐教室


外角公式 内角和公式和外角和公式 正多边形外角和公式 正n边形的内角和公式



十五角形 Pentadecagon Japaneseclass Jp



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


100以上正12角形三角形 壁紙引用画像hd



正十边形的画法步骤图 第1页 一起扣扣网



初一下册数学丨多边形的内角和与外角和 每日头条
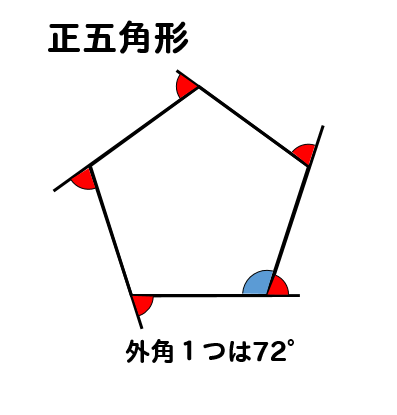


正多角形の1つの内角 外角を求める方法を問題解説 数スタ


Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


08年学业考试复习第一轮第四章基本图形一知识回顾多边形上或内部一点与多边形各顶点的连线将多边形分割成若干个小三角形如图给出了四边形的三种不同的分割方法分别将四边形分割成了2个3个4个小三角形



中2 図形の性質 多角形の外角の和 日本語版 Youtube


正九边形求内角 正多边形求内角的两种方法 腾讯视频



ラブリー六角形内角 ただぬりえ



内角和 内角和公式 五边形内角和 N边形内角和公式


中考数学复习第5章四边形第21讲多边形与平行四边形课件 图文 百度文库



ベストコレクション 正12角形三角形 Hd壁紙画像fhd


青少年编程 用python探究数学 3 老齐教室


18年10月29日の記事 時空先生のドリルプリント
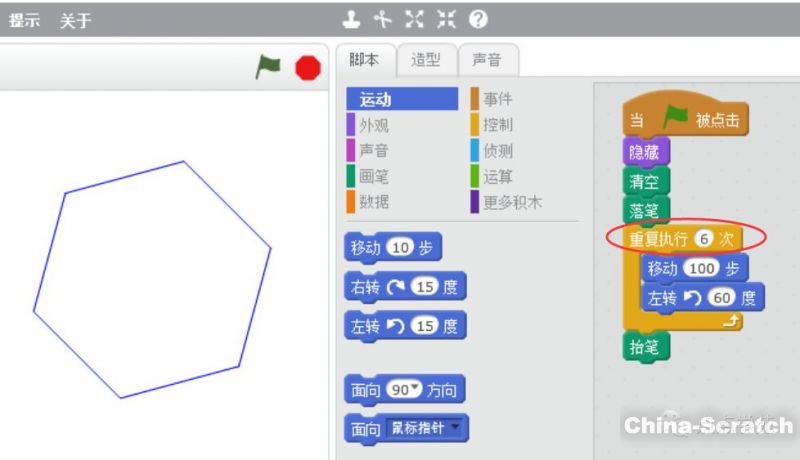


编程 Scratch 02 巧用scratch画正多边形 少儿编程教程网


求风筝图形内角度数 为什麽角2 角4如图案所示 2 4 5个风筝形拼成一个正10边形 所以 1 10 2 180 10 8 180 144 5 3 360 3 72 风筝形是个四边形 内角和是360度 并且 2 4 所以 作业 慧海网


课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅



壁紙押入れ 最高50 正12 角形
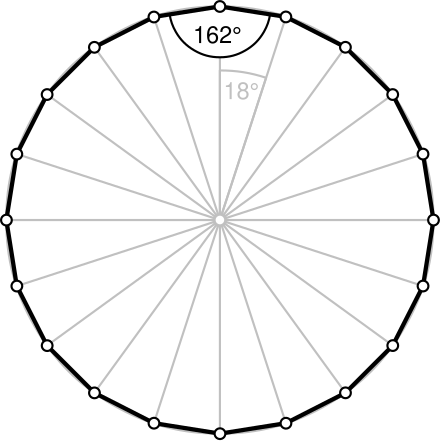


二十边形 Wikiwand


第四章多边形内角和



内角和公式 五边形内角和 多边形的外角和 N边形的内角和是



内角和 内角和公式 五边形内角和 N边形内角和公式



十边形怎么画简单 第1页 一起扣扣网


能力橙少儿编程 少儿编程小课 第十五课 正五边形



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



この問題がよく分かりません 分かる方なるべく早く解いてくれると嬉しいです Clear


五边形外角和等于多少 五边形的内角和是 正五边形的内角和 六边形内角和是多少



八年级下册数学 多边形的外角和 获奖教案设计下载 Docx 文档铺



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码



正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear
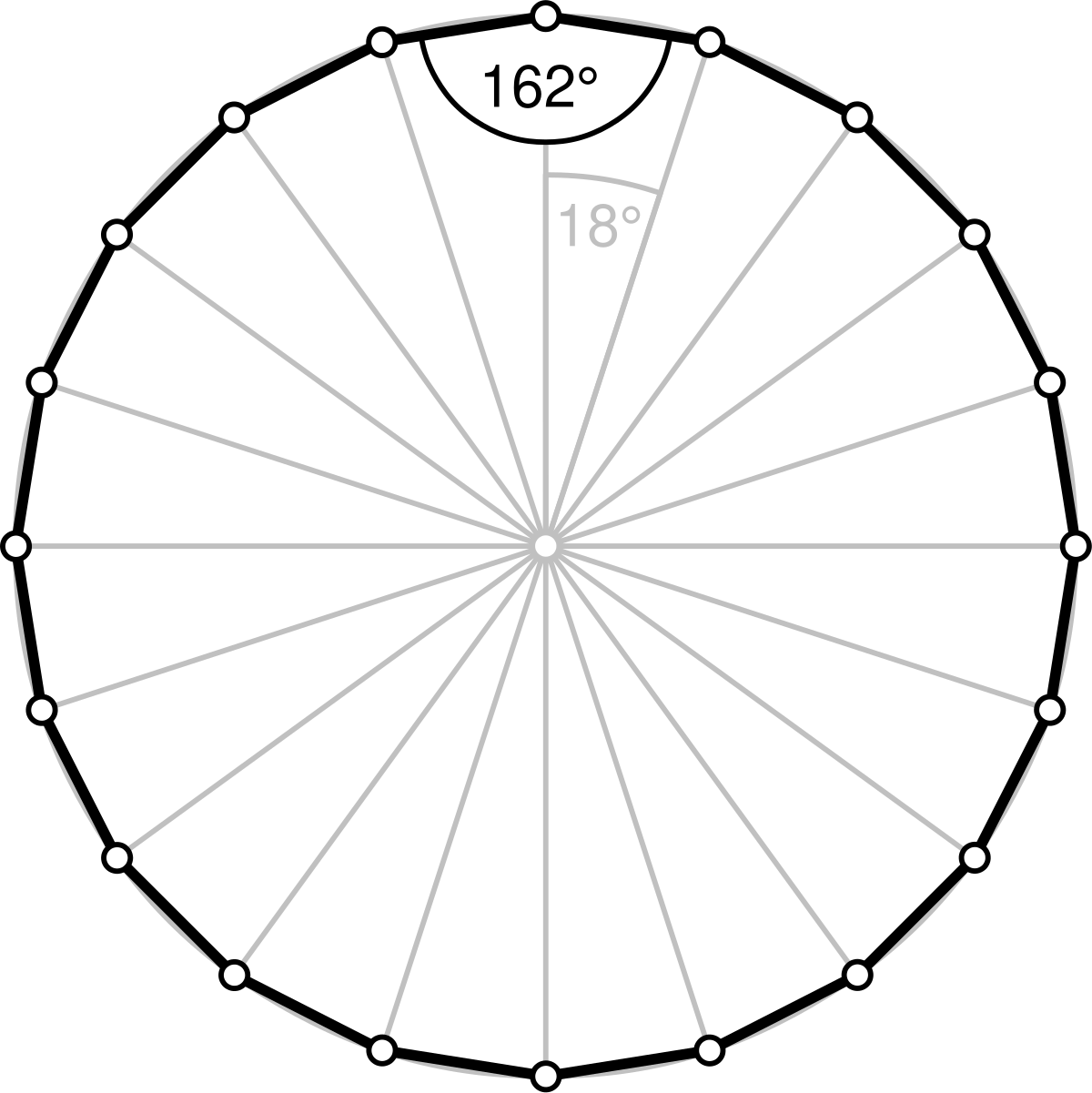


二十边形 维基百科 自由的百科全书



泡沫镍1 0 初级版 Cg杨杰图像设计 商业新知



中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく


十边形 维基百科 自由的百科全书


正五边形 腾讯视频



十边形怎么画简单 第1页 一起扣扣网



正方形的外角和是多少度



多角形の内角の和 外角の和の公式 数学fun


南山中学女子部過去問題演習



Python Turtle 画正多边形和多角形 弄斧人y Y的博客 Csdn博客 用python画正五边形的代码


南山中学女子部過去問題演習



觀念 N 邊形外角和定理 三角形的內角與外角 均一教育平台



十边形 维基百科 自由的百科全书



初一下册数学丨多边形的内角和与外角和 每日头条



二十边形 Wikiwand



外角公式 内角和公式和外角和公式 正多边形外角和公式 正n边形的内角和公式



正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム


100以上正12角形外角 リタ ベルナル


课件 教员分享 Z1版 七年级数学 沪教版 八年级下 22 1 探索多边形的内角和 免费数学课件下载 优思教辅


陈省身 三角形的内角和等于180 不对



八边形 Wikiwand


